Scott continuity
In mathematics, given two partially ordered sets P and Q a function 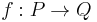 between them is Scott-continuous (named after the mathematician Dana Scott) if it preserves all directed suprema, i.e. if for every directed subset D of P with supremum in P its image has a supremum in Q, and that supremum is the image of the supremum of D: sup f(D) = f(sup D).[1]
between them is Scott-continuous (named after the mathematician Dana Scott) if it preserves all directed suprema, i.e. if for every directed subset D of P with supremum in P its image has a supremum in Q, and that supremum is the image of the supremum of D: sup f(D) = f(sup D).[1]
A subset O of a partially ordered set P is called Scott-open if it is an upper set and if it is inaccessible by directed joins, i.e. if all directed sets D with supremum in O have non-empty intersection with O. The Scott-open subsets of a partially ordered set P form a topology on P, the Scott topology. A function between partially ordered sets is Scott-continuous if and only if it is continuous with respect to the Scott topology.[1]
The Scott topology was first defined by Dana Scott for complete lattices and later defined for arbitrary partially ordered sets.[2]
Scott-continuous functions show up in the study of the denotational semantics of computer programs.
Contents |
Properties
A Scott-continuous function is always monotonic.
A subset of a partially ordered set is closed with respect to the Scott topology induced by the partial order if and only if it is a lower set and closed under suprema of directed subsets.[3]
A directed complete partial order (dcpo) with the Scott topology is always a Kolmogorov space (i.e., it satisfies the T0 separation axiom).[3] However, a dcpo with the Scott topology is a Hausdorff space if and only if the order is trivial.[3] The Scott-open sets form a complete lattice when ordered by inclusion.[4]
For any topological space satisfying the T0 separation axiom, the topology induces an order relation on that space, the specialization order: x ≤ y if and only if every open neighbourhood of x is also an open neighbourhood of y. The order relation of a dcpo D can be reconstructed from the Scott-open sets as the specialization order induced by the Scott topology. However, a dcpo equipped with the Scott topology need not be sober: The specialization order induced by the topology of a sober space makes that space into a dcpo, but the Scott topology derived from this order is finer than the original topology.[3]
Examples
The open sets in a given topological space when ordered by inclusion form a lattice on which the Scott topology can be defined. A subset X of a topological space T is compact with respect to the topology on T (in the sense that every open cover of X contains a finite subcover of X) if and only if the set of open neighbourhoods of X is open with respect to the Scott topology.[4]
For CPO, the cartesian closed category of complete partial orders, two particularly notable examples of Scott-continuous functions are curry and apply.[5]
See also
Footnotes
- ^ a b Vickers, Steven (1989). Topology via Logic. Cambridge University Press. ISBN 0-521-36062-5.
- ^ Scott, Dana (1972). "Continuous lattices". In Lawvere, Bill. Toposes, Algebraic Geometry and Logic. Lecture Notes in Mathematics. 274. Springer-Verlag.
- ^ a b c d Abramsky, S.; Jung, A. (1994). "Domain theory". In Abramsky, S.; Gabbay, D.M.; Maibaum, T.S.E.. Handbook of Logic in Computer Science. Vol. III. Oxford University Press. ISBN 0-19-853762-X. http://www.cs.bham.ac.uk/~axj/pub/papers/handy1.pdf.
- ^ a b Bauer, Andrej and Taylor, Paul (2009). "The Dedekind Reals in Abstract Stone Duality". Mathematical Structures in Computer Science (Cambridge University Press) 19: 757–838. doi:10.1017/S0960129509007695. http://PaulTaylor.EU/ASD/dedras/. Retrieved October 8, 2010.
- ^ Barendregt, H.P. (1984). The Lambda Calculus. North-Holland. ISBN 0-444-87508-5. (See theorems 1.2.13, 1.2.14)